A Polygon is a two-dimensional surface stored as a sequence of points defining an exterior bounding ring and zero or more interior rings. A Polygon instance can be formed from a ring that has at least three distinct points. The exterior and any interior rings of a Polygon define its boundary. The space within the rings defines the interior of the Polygon.

Polygons are two dimensional geometries, they have an associated length and area. The length of a polygon is measured as the sum of the distances between all consecutive points in all exterior and all interior rings (in other words the length of the shoreline). The area is the area contained within the exterior ring excluding the area contained in the interior rings.

Figure 1 shows example polygon geometries (1) is a polygon instance whose boundary is defined by an exterior ring. (2) is a polygon instance whose boundary is defined by an exterior ring and two interior rings. The area inside the interior rings is part of the exterior of the Polygon instance.(3) is a valid Polygon instance because its interior rings intersect at a single tangent point.

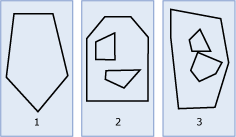
Figure 1: Example of polygon geometries

When polygons are used to define the shape of an object in a geographic coordinate system it is not trivial to classify what is the interior an the exterior area.